How to install talkd on Raspbian

Are you looking for install talkd daemon on Raspbian?

I will try to explain how to install it but before we start i just want to give a short explanation of what talkd is: it is the daemon that allow users to talk eachothers on the same machine.

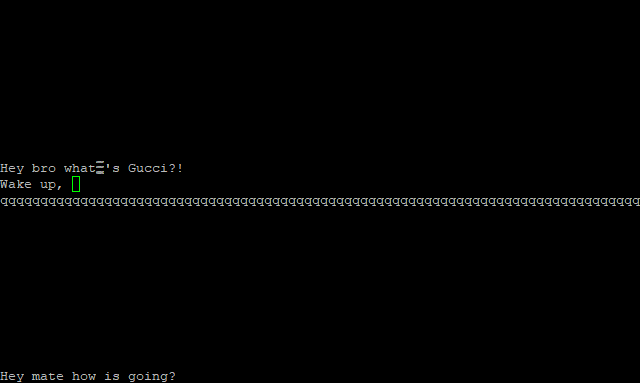
Going to the code, here how to install talkd on a raspberry pi: first you need to install all the packages that we need for with the following code:

$ sudo apt-get install talk talkd

After that you will need to modify /etc/hosts.allow adding this line:

talkd: 127.0.0.1

Now try it.
Login with different users on the same machine and:

$ mesg y
$ talk user@localhost

“mesg y” allows write access in your terminal

Discover More Raspberry Pi Tutorials and Guides!

Looking for more Raspberry Pi resources? Check out my comprehensive Raspberry Pi Tutorials and Guides page, where you’ll find a wide range of articles covering everything from basic setup to advanced projects. Whether you’re a beginner or an experienced user, my tutorials have something for everyone. Don’t miss out on the latest tips and tricks – explore my Raspberry Pi Tutorials and Guides page now!

🚀 Dive into our Raspberry Pi Tutorials and Guides!